Some Special Limits
Here we will discuss some important limits that everyone should be aware of. They are very useful in many branches of science.
Example: Show using the Logarithmic function that
,
for any a > 0.
Answer: Set 
. We have
. ln(a)
Clearly, we have
.
Hence,
which translates into
.
Example: Show that
.
Answer: We will make use of the integral while the Hôpital Rule would have done a cleaner job. We have
so
.
For 
, we have 
, which is equivalent to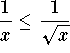 
. Hence,
.
But,
.
Therefore, putting the stuff together, we arrive at
.
Since,
,
as n goes to 
and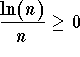 
, the Pinching Theorem gives
.
The difficulty in this example was that both the numerator and denominator grow when n gets large. But, what this conclusion shows is that n grows more powerfully than 
.
As a direct application of the above limit, we get the next one:
Example: Show that
.
Answer: Set 
. We have
.
Clearly, we have (from above)
.
Hence,
,
which translates into
.
The next limit is extremely important and I urge the reader to be aware of it all the time.
Example: Show that
,
for any number a.
Answer: There are many ways to see this. We will choose one that involves a calculus technique. Let us note that it is equivalent to show that
.
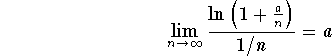Do not worry about the domain of 
, since for large n, the expression 
will be a positive number (close to 1). Consider the function
and f(0) = 1. Using the definition of the derivative of 
, we see that f(x) is continuous at 0, that is, 
. Hence, for any sequence 
which converges to 0, we have
.
Now, set
.
Clearly we have 
. Therefore, we have
.
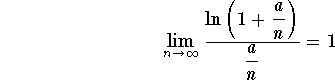But, we have
,
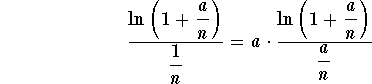which clearly implies
.
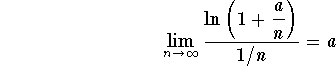Since
,
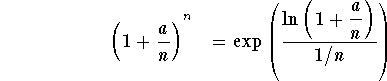we get
.
The next example, is interesting because it deals with the new notion of series.
Example: Show that
Answer: There are many ways to handle this sequence. Let us use calculus techniques again. Consider the function
.
We have
and
,
for any 
. Note that for any 
, we have
,
hence
,
which gives
.
Since
,
we get
.
In particular, we have
.
Therefore, since 
, we must have
.