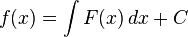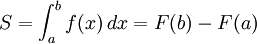matematikhocasi 0 554 581 39 64

İntegral

$int dx = x + C$

$int x^n,{rm d}x = frac{x^{n+1}}{n+1} + Cqquadmbox{ eğer }n ne -1$

$int {dx over x} = ln{left|xright|} + C$

$int {dx over {a^2+x^2}} = {1 over a}arctan {x over a} + C$

$int {dx over sqrt{a^2-x^2}} = arcsin {x over a} + C$

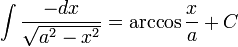
$int {-dx over sqrt{a^2-x^2}} = arccos {x over a} + C$

$int {dx over x sqrt{x^2-a^2}} = {1 over a} sec {|x| over a} + C$

$int ln(x) ,dx = x ln(x) - x + C,$

$int log_b {x},dx = xlog_b {x} - xlog_b {e} + C$

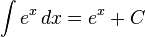
$int e^x,dx = e^x + C$

$int a^x,dx = frac{a^x}{ln{a}} + C$

$int a^{ln(x)},dx =int x^{ln(a)},dx=frac{x,a^{ln(x)}}{ln{a}+1} + C=frac{x,x^{ln(a)}}{ln{a}+1} + C$
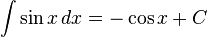
$int sin{x}, dx = -cos{x} + C$

$int cos{x}, dx = sin{x} + C$

$int tan{x} , dx = -ln{left| cos {x} right|} + C$

$int cot{x} , dx = ln{left| sin{x} right|} + C$

$int sec{x} , dx = ln{left| sec{x} + tan{x}right|} + C$

$int csc{x} , dx = ln{left| csc{x} - cot{x}right|} + C$

$int sec^2 x , dx = tan x + C$

$int csc^2 x , dx = -cot x + C$

$int sec{x} , tan{x} , dx = sec{x} + C$

$int csc{x} , cot{x} , dx = - csc{x} + C$

$int sin^2 x , dx = frac{1}{2}(x - sin x cos x) + C$

$int cos^2 x , dx = frac{1}{2}(x + sin x cos x) + C$

$int sec^3 x , dx = frac{1}{2}sec x tan x + frac{1}{2}ln|sec x + tan x| + C$

$int sin^n x , dx = - frac{sin^{n-1} {x} cos {x}}{n} + frac{n-1}{n} int sin^{n-2}{x} , dx$

$int cos^n x , dx = frac{cos^{n-1} {x} sin {x}}{n} + frac{n-1}{n} int cos^{n-2}{x} , dx$

$int arctan{x} , dx = x , arctan{x} - frac{1}{2} ln{left| 1 + x^2right|} + C$

f : R → R ye tanımlı ve her noktada sürekli ve türevli bir fonksiyon olsun.

f'(x) = F(x) ise

$f(x) = int F(x),dx + C$

olur.

Belirli integral ise alt ve üst sınırlarla belirlendiğinden integral alma işleminden sonra sınırlar ilkel fonksiyona konularak birbirinden çıkarılır ve değer yani fonksiyonun o sınırlar arasında belirttiği alan bulunmuş olur.

Örneğin ; a'dan b'ye kadar F(x) fonksiyonun belirttiği alan (S) ya da alt sınırı : a , üst sınırı : b olan integralin değeri istenirse :

1 - İntegralin önündeki fonksiyonun integrali alınır.

$f(x) = int F(x),dx + C$

olarak bulunur.

2 - Bulunan f(x) fonksiyonuna önce üst sınır (b) verilerek f(b) bulunur.Sonra da alt sınır olan (a) verilir ve f(a) bulunur.

3 - Son aşamada f(b)-f(a) işlemi yapılarak istenen değer ( a ve b arasındaki F(x)'in belirttiği alan (S) ) bulunur.

$S = int_a^b f(x),dx = F(b)-F(a)$

ör. $int_4^53x + 2,dx =( frac{3}{2}x^2+2x)|_4^5=frac{31}{2}$